Theoretical background

Introduction

Newton's law of universal gravitation

The forces with which two spherical bodies of mass \(m\) and \(M\) attract each other due to the gravitational field is given by the equation:

These are central forces that is directed to the line that connects the centers of mass of the two bodies

Satellite speed in a circular orbit

If we take are the reference point the center of mass of the two bodies and \(M \gg m\) then the center of mass is very close to the center of mass of the body with the larger mass \(M\) and then this body is almost stationary and we can consider the motion of the body with mass \(m\).  Such an example can be the Sun for mass \(M\) and a planet with mass m as well as the satellites that are in orbit around the earth or another planet. The orbit of the body with mass m depending on the initial conditions it can be a conical section, i.e., line, cycle, ellipse, parabola and hyperbola. The most common case is that of an elliptical orbit and the simpler to study is that of a cyclic orbit. In that case for a distance r from the center of the body with mass \(M\) we can calculate the necessary velocity for the body with mass \(m\) to have a cyclic orbit by the following equation

$$F=m\frac{\upsilon^2}{r}$$ $$m\frac{\upsilon ^2}{r}=G\frac{Mm}{r^2}$$

For the pair the Sun and the Earth and assuming the orbit is cyclic then the velocity of Earth at its current mean distance is given by:

$$\upsilon_\mathrm{E}=\sqrt{G\frac{M}{R_\mathrm{E}}}$$

Substituting the known values  \(GM=μ=1.3275\cdot 10^{20}\ \mathrm{m^3/s^2}\), \(R_\mathrm{E}=1.496\cdot10^{11}\mathrm{m}=1.00\ \mathrm{AU}\) we get:

Similarly for the Mars we get

$$\upsilon_\mathrm{M}=\sqrt{G\frac{M}{R_\mathrm{M}}}$$

Substituting the appropriate values  \(R_\mathrm{M}=2.279\cdot10^{11}\mathrm{m}=1.523\ \mathrm{AU}\) we get

Period calculation

The period of the body with mass m in cyclic orbit is:

$$\upsilon = \frac{2πr}{T}$$ $$\sqrt{G\frac{M}{r}}=\frac{2πr}{T}$$ $$G\frac{M}{r}=\frac{4π^2r^2}{T^2}$$

This equation, although it can derived assuming a cyclic orbit, is also valid for an elliptic or-bit.  It the latter case we have to replace the distance from the body with mass M by half the length of the major axis of the elliptic orbit, let us denote it by α, i.e.

The values for the Earth and for Mars are

and

Kepler's 3rd Law

From equation \( (3) \) we can easily come to

which is Kepler's 3rd law.

If the period is measured in Earth years \((\mathrm {years})\) and distances to \(\mathrm{AU}\) then applying the above equation for Earth with  \(a_\mathrm{E}=1\ \mathrm{AU}\) και \(T_\mathrm{E}=1\ \mathrm{year}\) we get

$$\frac{T^2}{a^3}=1$$ $$T=a\sqrt{a}\qquad \left (T\to \mathrm {years},\ \ a\to \mathrm{AU}\right )$$ From the equation above we can very easily calculate the period of a celestial body if we know the length of the semi-major Axis of its elliptical orbit.

Hohmann transfer

Sending a spacecraft from earth to another planet has a very high cost and even higher for a spaceship carrying humans.  Therefore, we have to engineer the path of the spaceship in such a way as to find the path with the minimum cost. In the following we will take into consideration only the cost that is needed to accelerate the spacecraft from a cyclic orbit around the earth on a path to meet Mars and when it reaches Mars to accelerate again to reach the orbit velocity of Mars around the Sun. To keep the calculation as simple as possible we can assume that both Earth and Mars have cyclic orbit around the Sun. The spacecraft while on Earth or on orbit around her it has almost the same velocity as that of the Earth, i.e.,  \(\upsilon_\mathrm{E}\). We have to accelerate the spacecraft to a new speed, i.e., \(\upsilon_1\) so as to reach Mars with no other path correction and after some time traveling with the engines shut it crosses the orbit of Mars with a velocity \(\upsilon_2\). At this point the engines should start again an accelerate the spacecraft to reach the orbital velocity of Mars, i.e \(\upsilon_2\) to \(\upsilon_\mathrm{M}\) .

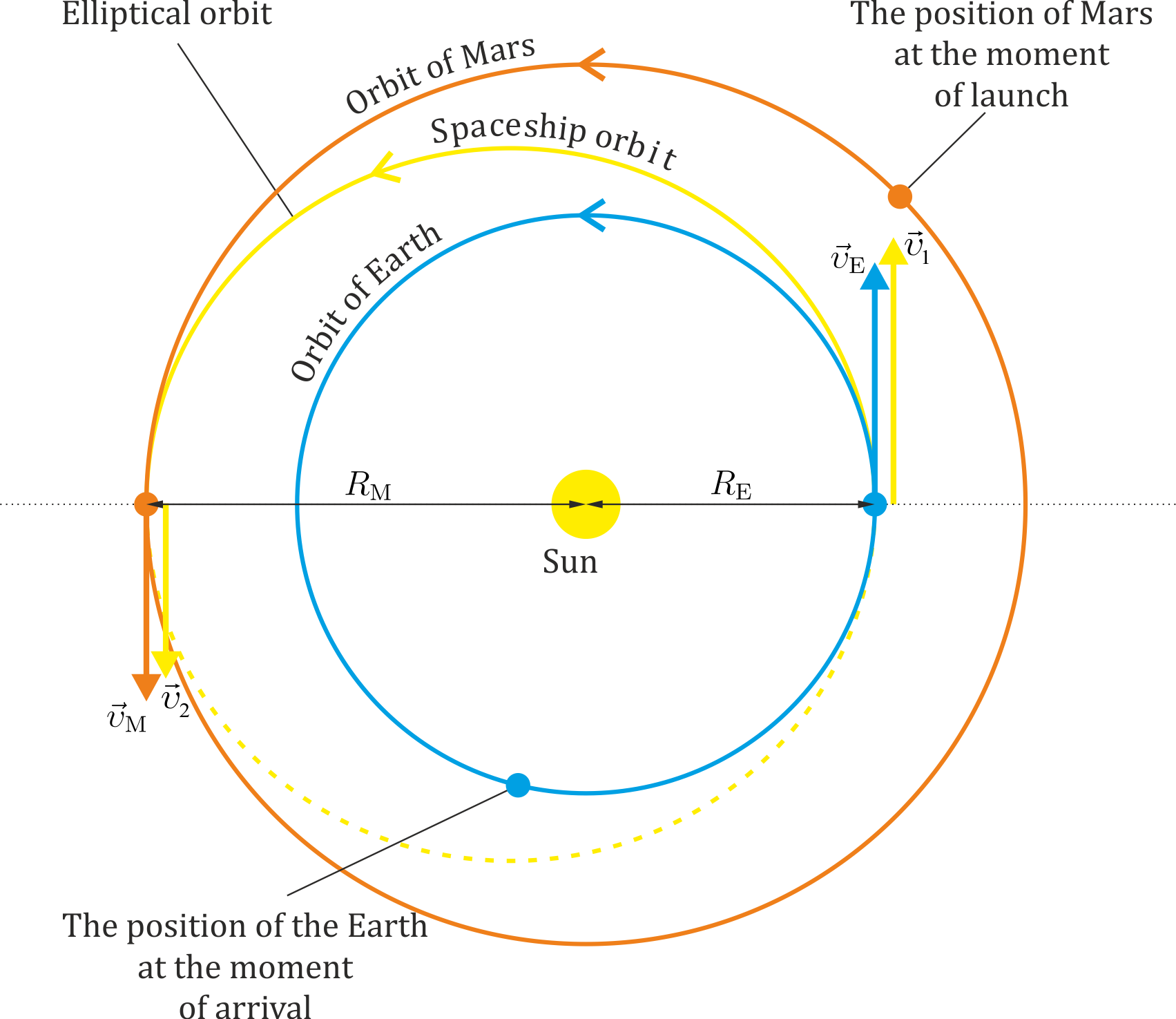
Calculation of required speed

By resorting the conservation of angular momentum of the spacecraft for the closest (perihelion) and the farthest point (aphelion) of the path we can find that speed of the spacecraft when it reaches Mars, which is

$$m\upsilon_1 R_\mathrm{E}=m\upsilon_2 R_\mathrm{M}$$

From the conservation of the total mechanical energy at the two points of the path (perihelion and aphelion) we can calculate the velocity 

Substituting the appropriate values \(GM=μ=1.3275\cdot 10^{20}\ \mathrm{m^3/s^2}\), \(R_\mathrm{E}=1.496\cdot10^{11}\mathrm{m}\), \(R_\mathrm{M}=2.279\cdot10^{11}\mathrm{m}\)

For the spacecraft to reach Mars with the described path we have to change its velocity from  \(\upsilon_\mathrm{E}=29.78\ \mathrm{km/s}\) σε \(\upsilon_1=32.73\ \mathrm{km/s}\) i.e

$$\Delta\upsilon_1=\upsilon_1-\upsilon_\mathrm{E}$$ $$\Delta\upsilon_1 = \left(32.73-29.79\right)\ \mathrm{km/s}$$ $$\Delta\upsilon_1 = +2.94\ \mathrm{km/s}$$

While  \(\upsilon_2\) will be

$$\upsilon_2=\frac{R_Γ}{R_\mathrm{M}}\upsilon_1$$ $$\upsilon_2=21.48\ \mathrm{km/s}$$

For the spacecraft to acquire the same cyclical orbit as Mars it has to increase its speed from  \(\upsilon_2=21.48\ \mathrm{km/s}\) σε

$$\Delta\upsilon_2=\upsilon_\mathrm{M}\upsilon_2$$ $$\Delta\upsilon_2 = \left(24.13-21.48\right)\ \mathrm{km/s}$$ $$\Delta\upsilon_2 = +2.65\ \mathrm{km/s}$$

Duration of the Hohmann transfer

The time needed for the spacecraft to reach Mars is half the period of the elliptic orbit that the Hohmann transfer employes:

$$Δt=\frac12 T_{\mathrm{spacecraft}}$$ $$Δt=\frac12 2π\sqrt{\frac{a^3}{GM}}$$

 \(a=\frac{R_\mathrm{E}+R_\mathrm{M}}{2}\) we get

$$Δt=258.78\ \mathrm{days}$$

At that time point of the path Mars would have ascribed and angle of

$$\Delta\theta=\frac{\Delta t}{T_\mathrm{M}}360°=135.6°$$

and the spacecraft \(180°\). Therefore, at the starting point of the Hohmann transfer Mars much precede Earth by \(\Delta\phi=180°-135.6°\) or 

$$\Delta\phi=44.4°$$

How long does it take for the conditions to be suitable for launch again?

The periods of Earth and Mars are :

$$T_\mathrm{E}=365.26\ \mathrm{days}$$ $$T_\mathrm{M}=686.97\ \mathrm{days}$$

ΑIf at a given instance the positions of Earths and Mars have an angle  \(\Delta\phi\) when viewed from the Sun then this can occur again after time  \(t\) determined by the condition 

$$ω_\mathrm{E}t-ω_\mathrm{M}t=2π$$ $$\frac{2π}{T_\mathrm{E}}t-\frac{2π}{T_\mathrm{M}}t=2π$$ $$\frac{T_\mathrm{M}-T_\mathrm{E}}{T_\mathrm{E}T_\mathrm{M}}t=1$$

$$t=780.0\ \mathrm{days}$$