Εισαγωγή στη πληροφορική και την ανοικτότητα
Περιγραφή θέματος
-
-
-
-
Σελίδα
-
Σελίδα
-
Λίστα ελέγχου
-
Σελίδα
-
Σελίδα
-
Ανάθεση εργασίας
-
Ανάθεση εργασίας
-
Ολόκληρο το κεφάλαιο σε μορφή pdf
-
-
Σελίδα
-
Ανάθεση εργασίας
-
Αρχείο
Ολόκληρο το κεφάλαιο 1.2 σε μορφή pdf
-
-
-
Σελίδα
-
Ανάθεση εργασίας
-
Ανάθεση εργασίας
-
Σελίδα
-
Ανάθεση εργασίας
-
Ανάθεση εργασίας
-
Αρχείο
-
-
-
-
Σελίδα
-
-
Ανοίξτε το παραπάνω αρχείο, μελετήστε το περιεχόμενό του και υλοποιήστε τα παρακάτω όπως αναφέρονται σε αυτό:
- Εγκατάσταση LibreOffice- Writer
- Εκκίνηση/Άνοιγμα LibreOffice- Writer
- Αποθήκευση αρχείου στο LibreOffice- Writer
Ορισμός περιθωρίων σελίδας
-
-
Ανοίξτε το παραπάνω αρχείο και ακολουθήστε τις οδηγίες του για να πληκτρολογήσετε και να μορφοποιήσετε βιωματικά το κείμενο της πρόσκλησης
-
Ανοίξτε το αρχείο "2.1.4 Εισαγωγή Εικόνας" και ακολουθείστε τις οδηγίες για την εισαγωγή του λογότυπου στην πρόσκληση.
-
Ανοίξτε το αρχείο "2.1.5 Αλλαγή διαστάσεων σελίδας (χαρτιού)" και ακολουθήστε τις οδηγίες για να ορίσετε τα περιθώρια του χαρτιού της πρόσκλησης.
-
Ανοίξτε το αρχείο " 2.1.6 Περίγραμμα σελίδας" και ακολουθήστε τις οδηγίες για να ορίσετε το περίγραμμα της πρόσκλησης.
-
Ανεβάστε στο Φόρουμ το αρχείο στο οποίο δημιουργήσατε τη μορφοποιημένη πρόσκληση που ολοκληρώσατε “libreoffice_επώνυμο_δραστηριότητα_πρόσκληση” (βάζετε το δικό σας επώνυμο)
-
Ανάθεση εργασίαςΆνοιξε: Δευτέρα, 10 Απριλίου 2023, 12:00 AM
 Στο έγγραφο που δημιουργήσαμε,
με τα εργαλεία του προγράμματος:
Στο έγγραφο που δημιουργήσαμε,
με τα εργαλεία του προγράμματος:1) Να βρείτε τη λέξη Ο.Α.Ε.Δ. και να την χρωματίσετε κόκκινη
2) Να αντικαταστήσετε τη λέξη Περιστερίου ή ΠΕΡΙΣΤΕΡΙΟΥ, με τη φράση Δήμου Περιστερίου.
3) Να αναιρέσετε την πρώτη ενέργεια αναίρεσης
4) Να επεξεργασθείτε το λογότυπο ώστε το κείμενό του να παρατίθεται στο δεξιό μέρος του όπως το κοιτάμε
-
Εδώ μπορείτε να βρείτε ολόκληρο ο υλικό του κεφαλαίου και το υπόλοιπο πολυμεσικό υλικό
-
-
Αρχείο
-
-
-
Αρχείο
-
Φάκελος
-
-
-
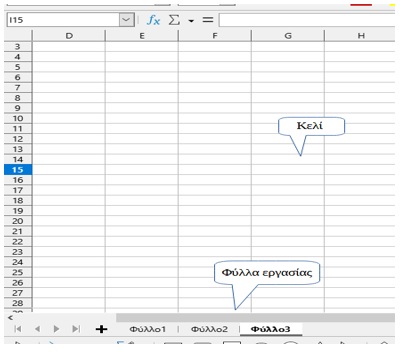
Ανοίξτε το αρχείο " 3.1.1.1. ΕΚΚΙΝΗΣΗ -ΠΕΡΙΒΑΛΛΟΝ LIBREOFICE CALC.pdf" και ακολουθήστε τις οδηγίες για να ανοίξετε και να γνωρίσετε περιβάλλον LibreOffice Calc, όπως και να αποθηκεύσετε αρχεία (λογιστικά φύλλα) στο ίδιο περιβάλλον.
-
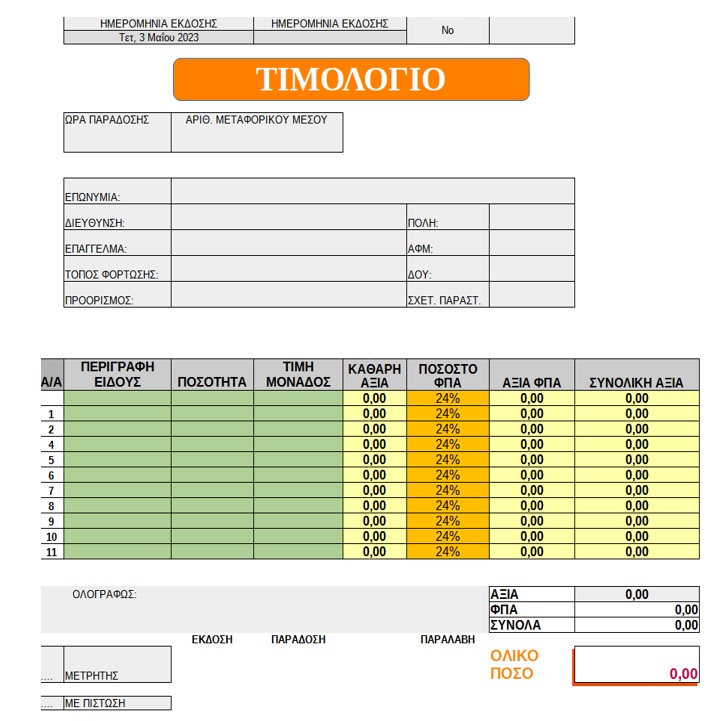
Ανοίξτε το αρχείο " 3.1.1.2 Δημιουργία, Άνοιγμα Βιβλίου εργασίας- Πληκτρολόγηση τιμολογίου.pdf" και ακολουθήστε τις οδηγίες για να δημιουργήσετε βιβλία στο LibreOffice Calc και να πληκτρολογήσετε περιεχόμενο σε ένα βιβλίο/αρχείο (πληκτρολόγηση περιεχομένου σε ένα τιμολόγιο).
-
Ανοίξτε το αρχείο "3.1.1.3 Επεξεργασία κελιών.pcf" και ακολουθήστε τις οδηγίες για να μάθετε πως επεξεργαζόμαστε τα κελιά σε ένα λογιστικό φύλλο στο LibreOffice Calc.
-
Για να μάθετε να εισάγετε και να μορφοποιείτε ένα σχήμα ή μια εικόνα στο LibreOffice Calc , ανοίξτε και ακολουθήστε τις οδηγίες του αρχείου "3.1.1.4 Εισαγωγή σχήματος – εικόνας"
-
Ακολουθώντας τις οδηγίες του αρχείου " 3.1.1.5 Μορφοποίηση αριθμών", μπορείτε στο LibreOffice Calc να μάθετε με μαρφοποιείτε αριθμούς , με βιωματικό τρόπο όπως συμβαίνει σε ολόκληρο το παρόν μάθημα.
-
Στο LibreOffice Calc μπορείτε εύκολα να συμπληρώνετε μια λίστα με αυτόματο τρόπο. Ανοίξτε το αρχείο " 3.1.1.6 Λίστα και Αυτόματη συμπλήρωση" και ακολουθήστε τις οδηγίες που σας δίνονται σε αυτό, για γνωρίσετε τι εννοούμε με τον όρο λίστα στα λογιστικά φύλλα και πως μπορείτε να τις συμπληρώνετε αυτόματα στο LibreOffice Calc.
-
Στο αρχείο "3.1.1.7 Απλοί Υπολογισμοί _Αυτόματη Άθροιση _Διόρθωση Τύπου" περιγράφονται αναλυτικά οι διαδικασίες που πρέπει να εφαρμόσετε, για να κάνετε απλούς υπολογισμούς, όπως αυτόματη άθροιση, διορθώσεις, να μάθετε τι είναι οι τύποι και πως να τους διορθώνετε , σε ένα λογιστικό φύλλο του LibreOffice, στο πλαίσιο της εφαρμογής ( (σύνταξη τιμολογίου) που υλοποιείτε τμηματικά και προοδευτικά
-
Φόρουμ
Ανεβάστε στο Φόρουμ "ΑΝΑΡΤΗΣΗ ΤΙΜΟΛΟΓΙΟΥ" το τιμολόγιο που δημιουργήσατε με άνομα αρχείου: “libreofficecalc_επώνυμο_δραστηριότητα_τιμολόγιο” (βάζετε το δικό σας επώνυμο)
-
Ανάθεση εργασίαςΆνοιξε: Σάββατο, 1 Ιουλίου 2023, 12:00 AM
 Δραστηριότητα 3.1 Να δημιουργήσετε ένα φύλλο εργασίας για τον υπολογισμό εξόδων σπιτιού όλου του χρόνου, όπως φαίνεται στην Εικόνα Δραστηριότητας1. Και αποθηκεύετε με το όνομα «ΕΞΟΔΑ 2023».
Δραστηριότητα 3.1 Να δημιουργήσετε ένα φύλλο εργασίας για τον υπολογισμό εξόδων σπιτιού όλου του χρόνου, όπως φαίνεται στην Εικόνα Δραστηριότητας1. Και αποθηκεύετε με το όνομα «ΕΞΟΔΑ 2023».Για την δημιουργία του παραπάνω φύλλου εργασίας θα λάβετε υπόψη ότι:
1. Οι μήνες και ο Α/Α θα δημιουργηθούν με αυτόματη συμπλήρωση.
2. Η μορφή των αριθμών θα είναι χωρισμένοι σε χιλιάδες, με 2 δεκαδικά και στο τέλος του αριθμού θα εισάγετε το σύμβολο του €.
3. Όλα τα Σύνολα θα γίνονται με χρήση της συνάρτησης Άθροιση.
4. Όλα τα έγχρωμα κελιά είναι γραμμένα ή προγραμματισμένα από τον δημιουργό του φύλλου εργασίας. Ο χρήστης εισάγει τιμές στα λευκά κελιά μόνο.
-
-
-
-
Αρχείο
-
Φάκελος
-
-
-
Φάκελος
-






 Γνωρίζεις τι είναι το
LibreOffice-Writer;
Γνωρίζεις τι είναι το
LibreOffice-Writer;